491. 递增子序列

Similar Question

Solution Tips

方案一: 回溯 + N 叉树 + 哈希表

用哈希表记录每个解, 避免重复, 但是空间复杂度和时间复杂度都太高了

var findSubsequences = function (nums) {
    const res = [];
    // 不能排序了
    // nums.sort((a, b) => a - b);
    const resMap = {};
    dfs([], 0);
    return res;


    function dfs(chosen, index) {
        if (index === nums.length) {
            return;
        }

        for (let i = index; i < nums.length; i++) {
            if (i > 0 && nums[i] >= chosen[chosen.length - 1]) {
                // 满足非递增的才 push
                chosen.push(nums[i]);
                if (chosen.length > 1 && !resMap[chosen.join(',')]) {
                    res.push([...chosen])
                    resMap[chosen.join(',')] = true;
                }
                dfs(chosen, i + 1);
                chosen.pop();
            }
            else if (chosen.length === 0) {
                // 为空时直接 push 一个数
                chosen.push(nums[i]);
                dfs(chosen, i + 1);
                chosen.pop();
            }
        }
    }
};
console.log(findSubsequences([1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]));

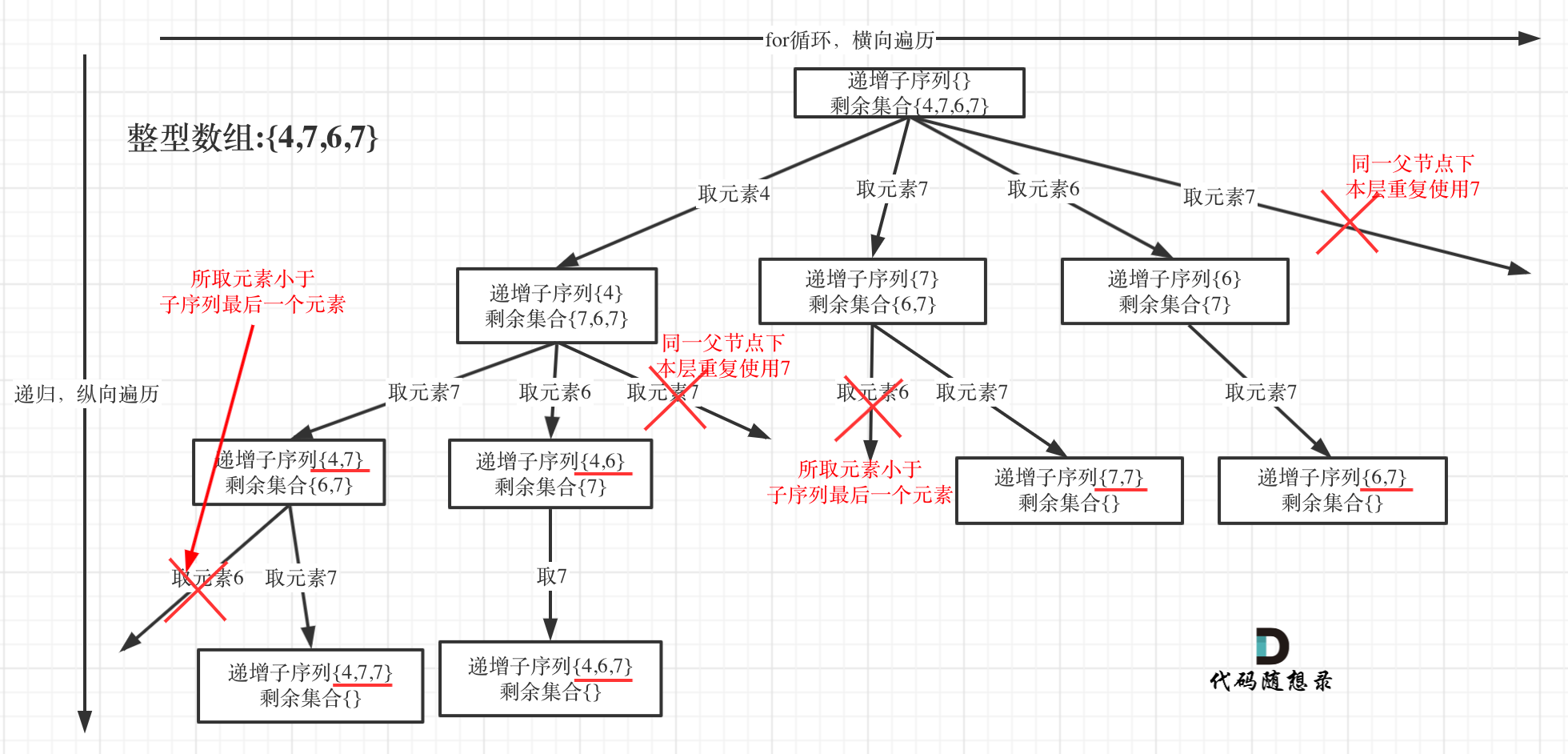
方案一优化: 单层哈希表

其实只需要同一层不选取重复的数字即可

var findSubsequences = function(nums) {
    let result = []
    let path = []
    function backtracing(startIndex) {
        if(path.length > 1) {
            result.push(path.slice())
        }
        let uset = []
        for(let i = startIndex; i < nums.length; i++) {
            if((path.length > 0 && nums[i] < path[path.length - 1]) || uset[nums[i] + 100]) {
                continue
            }
            uset[nums[i] + 100] = true
            path.push(nums[i])
            backtracing(i + 1)
            path.pop()
        }
    }
    backtracing(0)
    return result
};

方案二: 二元思想 + 分类讨论

我们可以对选择和不选择做一些简单的限定，就可以让枚举出来的都是合法的并且不重复：

使序列合法的办法非常简单，即给「选择」做一个限定条件，只有当前的元素大于等于上一个选择的元素的时候才能选择这个元素，这样枚举出来的所有元素都是合法的

那如何保证没有重复呢？我们需要给「不选择」做一个限定条件，只有当当前的元素不等于上一个选择的元素的时候，才考虑不选择当前元素，直接递归后面的元素。因为如果有两个相同的元素，我们会考虑这样四种情况：

1. 前者被选择，后者被选择
2. 前者被选择，后者不被选择
3. 前者不被选择，后者被选择
4. 前者不被选择，后者不被选择

其中第二种情况和第三种情况其实是等价的，我们这样限制之后，舍弃了第二种，保留了第三种，于是达到了去重的目的。

这方案好难理解呀, 为啥就可以跳过重复呢

var findSubsequences = function (nums) {
    const res = [];
    dfs([Number.MIN_SAFE_INTEGER], 0);
    return res;


    function dfs(chosen, index) {
        if (index === nums.length) {
            if (chosen.length >= 2) {
                res.push(chosen.slice(1));
            }
            return;
        }

		// 符合题意, 并且选择的 case
        if (nums[index] >= chosen[chosen.length - 1]) {
            chosen.push(nums[index]);
            dfs(chosen, index + 1);
            chosen.pop();
        }

		// 不选择的 case
		// 两个元素相等的时候，选择了第一个那么第二个也一定被选中。如果没选择第一个，那么第二个可以被选也可以不被选
		// 4 6 7 7 中的 467, 7 是第二个 7
		// 因为总是存在某一时刻已经有 467 了, 然后又看到了第二个7, 此时不会执行dfs, 而是直接 pop 了第一个 7 出来
        if (nums[index] !== chosen[chosen.length - 1]) {
            dfs(chosen, index + 1);
        }
    }
};

方案三: 二进制枚举

Loading Question... - 力扣（LeetCode）